数学教育専修 教育学部

深い数学の背景を踏まえた、算数・数学に関する指導力に優れる人間性豊かな教員を養成することを目指します。

学びのポイント

• 

  1 ．数学の内容とともに、その指導法を学びます

  数学は一般には難解な教科と思われ がちですが、自然現象や社会現象のいろいろな法則を知るために欠かせない教科で、日常や社会生活に必要な学びがあり、理解できればこんなに楽しく明快なものはありません。
  　数学教育専修では、大学4年間で人類が培ってきた数学の体系の一端に触れるとともに、数学の内容及びその指導法について学びます。学習を通して、数学的な見方や考え方を身に付け、教育についての自らの理想を高め、指導力に優れた教員を目指しましょう。

• 

  2 ．常に考える姿勢で取り組みます

  数学教育専修を希望する学生には、数学を含 め、いろいろな分野に興味・関心を持ち、客観的に物事を捉えることができる能力を備えていること、また、他人のよさがわかる豊かな人間性を備えていることを希望します。昨今、学力低下が叫ばれ ていますが、まず学校の先生が自ら学ぶ姿勢を児童・生徒に示していくことが大切です。数学を理解するには、何度もチャレンジする姿勢が必要です。常に考え続ける姿勢で取り組みましょう。

•  

  3．数学研究会（学生の組織）

  　学生の組織として、数学教育講座には数学研究会があります。主な活動としては、半世紀以上にわたり続け てきた夏の算数・数学教室があります。カリキュラム外の活動ですが、活動を通して算数・数学を学ぶことのよさを共有し合うとともに、一つの目的に向かって計画的・組織的に教育活動を展開していくことの大切さを学びます。

学びの領域

各分野をバランスよく学びます

算数・数学の内容を通して児童生徒を育てていく数学教育、文字や記号を使って数の関係や性質を学ぶ代数学、物の形や大きさ・位置など空間に関する性質を研究する幾何学、高校で学んだ微分や積分をさらに進める解析学、数学の世界にコンピュータを活用するプログラミング、確率・統計をさらに深める分野などがあります。

数学教育専修の授業について

• 

  算数・数学教育実践演習I

  先輩方、先生と一緒に数学または数学教育について学びます。様々な考えを交流でき、とても深い学びができます

• 

  中等教科教育法IV（数学）

  学生同士で、中学数学または高校数学の一部の模擬授業を行い、授業研究をします。授業をする際はもちろん、他の学生の模擬授業を見て学ぶこともできます。

主な開講科目

線形代数／微分積分／数理プログラミング／情報数理基礎／数理統計I／図形と位相／初等教科教育法（算数）／算数・数学教育実践演習I・II／中等教科教育法III・IV（数学）／算数・数学教育実践演習III・IV／フーリエ解析／コンピュータと数学

授業の詳細はシラバスからご覧いただけます。「教育学部　シラバス」から科目名を検索のうえ、ご覧ください。

～教員による授業紹介コラム～

「数学教育基礎」近藤裕 先生（奈良教育大学Knowledge 授業コラム2022年掲載）

主に数学教育専修3回生が受講する、数学教育専修専門科目「数学教育基礎」についてご紹介します。

在学生の声

「『得意』を生かし、『好き』を深める」数学教育専修4回生　江藤啓太さん

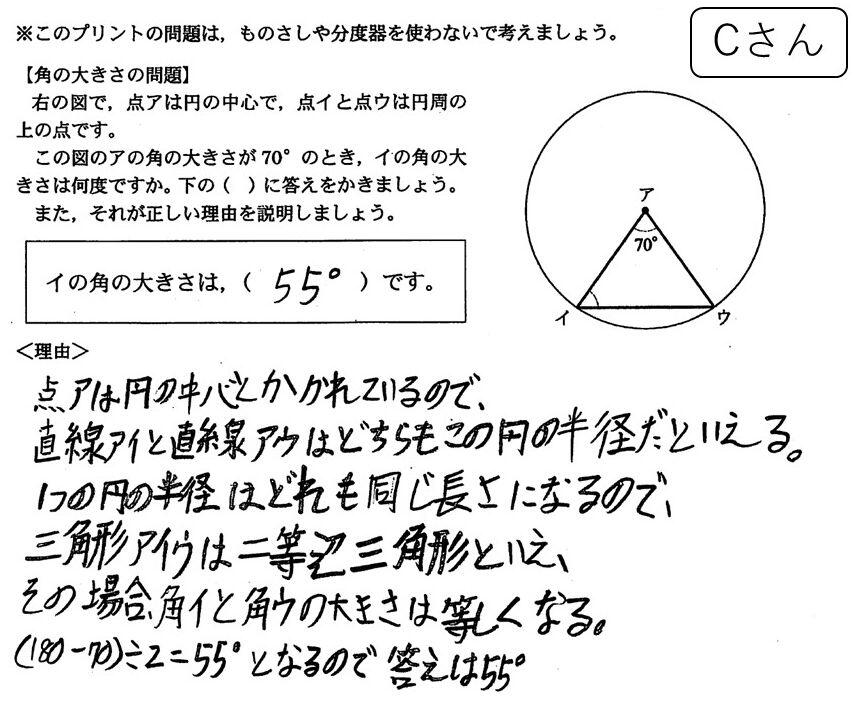
　数学教育専修では、高校までに学習した数学をもとに、より厳密で専門的な数学を扱う科目と、数学の指導法について学生同士の討議・実践等を中心に展開する科目とをバランスよく学ぶことができます。インプット（学ぶ・蓄積する）に増して、アウトプット（教える・伝える）する機会が多く設けられており、4年間を通して、総合的かつ多面的に数学の教科専門的な知識・視点を養うことができます。個性豊かで温かい先生方のもと、アットホームな環境で学べることも強みです。
　また、本学は複数の免許を取りやすい環境にあります。私は幼い頃からのピアノ演奏の特技を生かし、音楽科（中学・高校）の免許取得も目指して履修計画を組んできました。
　大学生活は自由度が高く、専門性の養成も含め、のびのびと『好き』や『得意』を伸長できます。この和やかな奈良の地で、私たちと共に学びませんか？

教育実習体験記

教育実習体験記はこちら　

学生による数学教育専修PR動画

2021年度作成（※所属や内容は作成当時のものです。）

取得できる免許状、卒業後の進路

取得できる免許状

・〔初等教育履修分野〕小学校教諭一種 等
・〔中等教育履修分野〕中学校教諭一種（数学） 等

数学教育専修の卒業生の教員免許状の取得実績はこちら

卒業後の主な進路

　中学校・高等学校教諭（数学）と小学校教諭が主な進路です。常勤講師、非常勤講師も合わせると、教員志望卒業生のほぼ100％が、各都道府県の公立・私立の教員となり、現在活躍しています。本学には大学院があり、学部卒業生も進学しています。そこでは、高度な専門職としての教員を目指して、学部の教育内容をさらに推し進め、自分のテーマを持って研究してゆくことになります。

教員採用試験合格体験談はこちら　

活躍する卒業生を紹介

・京都府立高等学校勤務（数学教育専修2018年3月卒業）（広報誌「ならやま」2020年秋 掲載）

教員および専門分野

教員の研究・研究室の紹介

教員の研究内容や研究室などについて、広報誌等で紹介した記事をご覧ください。※所属および記事の内容は、作成当時のものです。

• 「これまでの教育・研究と現在～不易を見つめなおす～」川崎謙一郎 先生（奈良教育大学Knowledge リレーコラム2021年掲載）
• 「数学を見直してみよう－微分方程式を交えて－」高橋亮 先生（広報誌「ならやま」2018年秋号掲載）
• 「微分方程式論の一端を覗く －自由落下運動と2次元点渦系を例に－」高橋亮 先生（E-book 2016年発行）
• 「世界の数学科授業・日本の数学科授業」舟橋友香 先生(E-book 2016年発行)

教員の研究内容をもっと知りたい方は、下記表の教員氏名をクリックし、教員個人ページ内の「研究シーズ」をご覧ください。また、「研究シーズ」一覧からもご覧いただけます。「研究シーズ」とは教員の研究内容をA4一枚にまとめたものです。（WEBからお読みいただけます）
奈良教育大学 大学教員「研究シーズ」一覧はこちら